Théorème de Huygens (pour un moment d'inertie)
Parfois, on dispose du moment d'inertie d'un solide par rapport à un axe passant par son centre de gravité, mais on souhaite obtenir le moment d'inertie de ce solide par rapport à un autre axe, parallèle au précédent.
Soit un axe \( \vec u\) passant par le centre de gravité G d'un solide S et un axe parallèle à \(\vec u\), à la distance \(d\) de \(\vec u\) et passant par le point A.
On cherche la relation entre \(I_{Gu}(S)\) et \(I_{Au}(S)\).
Définition : Théorème de Huygens
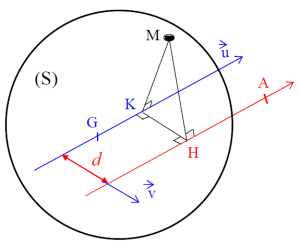
Complément : Démonstration du théorème de Huygens
\(I_{Au}(S) = \int_S \overrightarrow{HM}^2 \, dm = \int_S \left ( \overrightarrow{HK} + \overrightarrow{KM} \right) ^2 \, dm\)
\(=\int_S \overrightarrow{HK}^2 \, dm + \int_S \overrightarrow{KM}^2 \, dm + \int_S 2\, \overrightarrow{HK}.\overrightarrow{KM} \, dm\)
\(=m\, d^2 + I_{Gu}(S) + 2 \, \int_S 2\, \overrightarrow{HK}.\overrightarrow{KG} \, dm + 2\, \overrightarrow{HK}.\overrightarrow{GM} \, dm\)
Or : \(\overrightarrow{HK}.\overrightarrow{KG} = O\) et \(2\, \overrightarrow{HK}.\overrightarrow{GM} \, dm = 2 d \vec v \cdot \int_S \overrightarrow{GM} \, dm\)
Enfin : \(\int_S \overrightarrow{GM} \, dm = \vec 0\) par définition du centre de gravité.