Moments d'inertie d'un solide
Introduction
Considérations énergétiques
En considérant un point P de masse m en mouvement par rapport à un repère R, on peut écrire que l'énergie cinétique de ce point dans son mouvement relatif à R est \(E =\frac{1}{2} m V^2\). Si ce point P tourne autour d'un axe Δ fixe dans R, sa vitesse V est égale à r ω (avec r le rayon de la trajectoire circulaire). Ainsi, son énergie cinétique devient \(E = \frac{1}{2} m r^2 \omega ^2\).
Dans les deux expressions de l'énergie cinétique du point P, on retrouve toujours : à la fois une grandeur cinétique caractérisant la vitesse ( V ou ω ), et une grandeur d'inertie caractérisant la répartition de masse, propre au point ( m ou m r2 ).
C'est ce dernier terme : m r2 , qui est appelé moment d'inertie du point P par rapport à l'axe de rotation Δ.
Considérations dynamiques
Dans le chapitre traitant de la Dynamique, nous verrons qu'un corps subissant une action mécanique de type glisseur voit sa vitesse linéaire être modifiée : il accélère de manière rectiligne. C'est sa masse qui, finalement, caractérise sa capacité à résister à cette accélération linéaire. En effet, pour une même action mécanique de type glisseur, plus la masse du corps est grande, plus l'accélération linéaire est faible.
Ainsi, de manière analogue, nous verrons qu'un corps subissant une action mécanique de type moment voit sa vitesse angulaire être modifiée : il accélère de manière circulaire (ou angulaire).
C'est son moment d'inertie qui, finalement, caractérise sa capacité à résister à cette accélération angulaire. En effet, pour une même action mécanique de type moment, plus le moment d'inertie est grand, plus l'accélération angulaire est faible.
Définitions
Définition : Moment d'inertie par rapport à un axe Δ
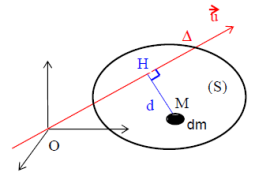
H = projection orthogonale de M appartenant à S sur Δ = (O, \(\vec u\))
d = distance de M à l'axe Δ
Définition : Moment d'inertie par rapport à un point O
Moments d'inertie dans un repère cartésien
Avec un point M de coordonnées (x, y, z) dans un repère \((O, \vec x, \vec y, \vec z)\) :
Remarques
Remarque :
Le moment d'inertie est donc une manière de caractériser la répartition de la masse d'un solide autour d'un point ou d'un axe. Si la majeure partie de sa masse est éloignée de ce point ou de cet axe, le moment d'inertie correspondant sera grand, et de manière proportionnelle au carré de la distance d'éloignement.
Pour un solide en rotation autour d'un axe : si son moment d'inertie autour de cet axe est faible, il atteindra sa vitesse de rotation nominale rapidement.
On cherche donc le plus souvent à réduire le moment d'inertie des axes des moteurs, car on veut la plupart du temps qu'ils atteignent leur vitesse de rotation nominale le plus rapidement possible. En revanche, dans certaines applications, on souhaite que le solide en rotation ait un grand moment d'inertie de façon à ce que sa vitesse de rotation varie le moins possible à cause des perturbations (cf. "volants d'inertie").