Théorème de Huygens (forme matricielle)
Ce théorème donne la relation existant entre \(\mathfrak{I}_G(S)\), matrice d'inertie du solide S au centre de gravité G, et \(\mathfrak{I}_P(S)\), matrice d'inertie du même solide en un autre point P, tel que \(\overrightarrow{PG} = x \vec x + y \vec y + z \vec z\)
La matrice d'inertie en un point quelconque P est la somme de :
la matrice d'inertie exprimée au centre de gravité G
la matrice d'inertie en P du point G affecté de la masse totale.
\[\mathfrak{I}_{\color{red}P} (S) = \mathfrak{I}_{\color{red}G}(S) + \left( \begin{array}{ccc} m \left( y^2 + z^2\right) & -mxy & -mxz \\-mxy & m \left( x^2 + z^2\right) & -myz \\ -mxz & -myz & m \left( x^2 + y^2\right) \end{array}\right)_{(\vec x,\vec y,\vec z)}\]
Exemple :
Matrice d'inertie d'un cylindre exprimée au centre de sa base :
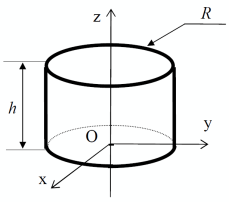
Cylindre d'axe de révolution z
\[\left( \begin{array}{ccc} m\left( \frac{R^2}{4}+ \frac{h^2}{3}\right ) & 0 & 0 \\0 & m\left( \frac{R^2}{4}+ \frac{h^2}{3}\right ) & 0 \\ 0 & 0 & m\left( \frac{R^2}{2}\right ) \end{array}\right)_{(-,-,\vec z)}\]
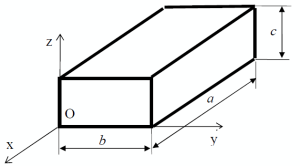
\[\left( \begin{array}{ccc} \frac{m}{3} \left( b^2 + c^2 \right) &\frac{mab}{4} & \frac{mac}{4} \\\frac{mab}{4} & \frac {m}{3} \left( a^2 + c^2 \right) & - \frac{mbc}{4} \\ \frac{mac}{4} & - \frac{mbc}{4} & \frac {m}{3}\left( a^2 + b^2 \right) \end{array} \right)_{(\vec x,\vec y,\vec z)}\]