Propriétés de la matrice d'inertie
Solide ayant un plan de symétrie
Si un solide possède un plan de symétrie, alors parmi les trois produits d'inertie de la matrice, seul celui défini par rapport au plan de symétrie n'est pas nul. L'axe perpendiculaire au plan de symétrie est un des axes principaux d'inertie.
Exemple :
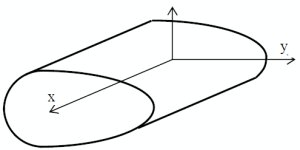
Soit le solide S symétrique par rapport au plan \((O,\vec x, \vec y)\). Les produits d'inertie \(P_{Oxz}\) et \(P_{Oyz}\) sont nuls, et l'axe \(\vec z\) est principal d'inertie.
La matrice d'inertie de S a alors la forme suivante :
Solide ayant un axe de révolution
Si un solide possède un axe de révolution, alors les deux moments d'inertie de la matrice correspondant aux deux autres axes (orthogonaux à l'axe de révolution) sont identiques.
De plus, tous les produits d'inertie sont nuls.
La matrice étant alors diagonale, le repère R est repère principale d'inertie. Par extension, tous les repères dont un axe est l'axe de révolution du solide, le sont aussi.
Exemple :
Soit le solide S possédant un axe de révolution \((O \vec z)\). Les produits d'inertie sont nuls, et les moments d'inertie suivant les axes \(\vec x\) et \(\vec y\) sont identiques.
La matrice d'inertie de S a alors la forme suivante :